How To Do Long Multiplication Sums (tu x tu) - Step by Step Guide - Quick Column Method
Maths and English worksheets for your child's year group, made by Sunita, an experienced UK primary school teacher. Print them at home and sit together for ten minutes.
Free trial, no card
Times tables and division worksheets for Year 3
Sign up free, pick your child's year group and print 3 worksheets this week. Made by a UK primary school teacher, yours to use at the kitchen table.
- ✓Made by an experienced UK primary school teacher
- ✓Mapped to the national curriculum, Reception to Year 6
- ✓Print at home and work on paper, no screen needed
No card needed. One teacher, every worksheet.
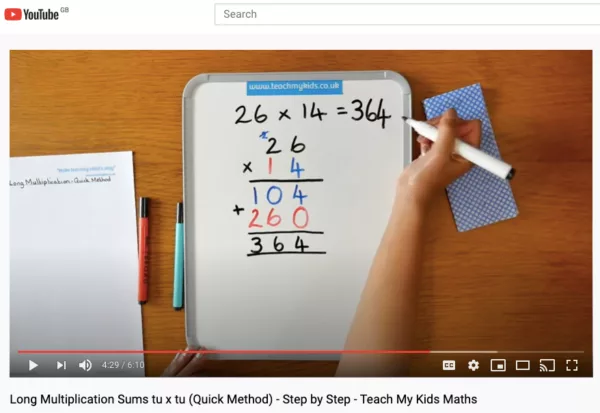
Long Multiplication sums (tu x tu) - Step by Step Explanation - Quick Method
Learning to multiply a 2 digit number by another 2 digit number can appear to be quite daunting. But once you understand the technique, you can easily multiply 2 or 3 digit numbers, using the column method, easily and quickly. There are many ways you can multiply larger numbers together e.g grid method, expanded column method, column method etc. Watch this video showing How to do a long multiplication sum using the column method.
Some children will find one method easier to understand and use. Children can be shown the different methods of multiplying numbers, this may help when they are first learning the principles behind long multiplication sums. Once they are more confident, they can then move onto the quick, efficient way of long multiplication sums. This will help them in tests and exams, where the time taken to work out a sum matters. Schools may teach how to solve long multiplication sums in a variety of ways.
Join Teach My Kids to gain access to a whole year's worth of Maths and English worksheets.
Long Multiplication Sums Explained Step by Step (Column Method)
Below is an example of how to work out a long multiplication sum using the quick, efficient column method.
Multiplication Sum: 43 x 12 =
- Write the numbers into columns. Remember to put the tens and units for each number underneath each other.
- 4 3
x 1 2
- First multiply 43 x 2
4 3
x 1 2 (2 x 3 = 6) then (2 x 4 = 8) Write the answers to these sums underneath, as you would in an addition sum.
8 6
There are no numbers to carry over, if there are numbers to carry over, this can be done in the same way you would with an addition sum.
- Next multiply 43 x 10
Although we are going to multiply 43 x 10, we will first place a 0 underneath the 6. We do this because we know that whenever a number is multiplied by 10 the answer ends in a 0.
We can then continue with the sum.
4 3
x 1 2
8 6
4 3 0 (1 x 3 = 3) then (1 x 4 = 4) Write the answers to these sums underneath, as you would in an addition sum.
In this example, there are no numbers to carry over. If there are numbers to carry over, this can be done in the same way you would with an addition sum.
- Finally add 86 + 430.
We start by adding the numbers in the units column first (6+0 = 6)
Add the tens (8+3=11). Notice the number 11, is made up of 1 ten and 1 unit, therefore we need to carry the 1 ten over to the hundreds column and write it into our sum.
Add the hundreds (1+4=5).
4 3
x 1 2
1 8 6
+ 4 3 0
5 1 6
The answer to 43 x 12 = 516
For more step by step examples on how to work out long multiplication sums using the column method visit Teach My Kids Learning Channel.
If you have found our Learn Multiplication video helpful, remember to 'Like' and hit the 'Subscribe' button on Teach My Kids Learning Channel.
Join Teach My Kids to gain access to a whole year's worth of Maths and English worksheets.
Who makes the worksheets
Sunita
UK primary teacher
Every worksheet on Teach My Kids is made by Sunita, a UK primary school teacher with over ten years in the classroom. She writes each one by hand and maps it to the national curriculum, so what your child practises at home lines up with what they do at school. It's all on paper, not a screen, and takes about ten minutes a day.
Try the classroom freeWhat you're joining
This is your child's online classroom.
You're not buying a single worksheet. You log in to a space set up for your child, where the full Year 3 library unlocks and everything stays in one place.
-
1.
Your own space, any time.
A login for your family. No app to install. Open it whenever suits you.
-
2.
Set to your child's year.
Pick their year group and the right worksheets unlock. Move it up as they grow.
-
3.
The whole library unlocks.
Every worksheet for their year in maths and English, matched to the school curriculum and sorted by topic. Not one sheet, all of them.
-
4.
Print what you need, when you need it.
The whole library is open, so you print this week's topics when they come up at school. No daily limit and nothing to ration. Come back as often as you like.
-
5.
Tick off what's done.
Mark each worksheet as done so you can see what your child has covered.
Common questions
Questions parents ask
- How do you do long multiplication?
- Set the two numbers out in columns. Multiply the top number by the units digit, then by the tens digit, writing each result on its own line. Add the two lines together for the answer. One step at a time keeps it tidy.
- How can I help my child learn their times tables?
- Short, regular practice works best. A few minutes a day, and mix the order so they are not just reciting. Spot the patterns, like the tens or the fives, and link division to the same facts so they see both at once.
- What is the column method for multiplication?
- It is a way of multiplying larger numbers by lining them up in columns and taking one digit at a time. Most primary schools teach it this way, and it keeps each step clear so mistakes are easier to spot.
From the kitchen table
From parents who already print at home.
Real parents, phonics through to SATs.
Putting Your Child's Education First
Worksheets by year and topic
- Reception maths worksheets
- Year 1 maths worksheets
- Year 2 maths worksheets
- Year 3 maths worksheets
- Year 4 maths worksheets
- Year 5 maths worksheets
- Year 6 maths worksheets
- Year 1 English worksheets
- Year 2 English worksheets
- Year 3 English worksheets
- Year 4 English worksheets
- Year 5 English worksheets
- Year 6 English worksheets
- Times tables worksheets
- Multiplication tables check
- Multiplication worksheets
- Division worksheets
- Fractions worksheets
- Decimals worksheets
- Percentages worksheets
- Place value worksheets
- Addition worksheets
- Subtraction worksheets
- Telling the time worksheets
- Shape worksheets
- Grammar worksheets
- Fronted adverbials
- Adverbs worksheets
- Nouns worksheets
- Verbs worksheets
- Adjectives worksheets
- Spelling worksheets
- Handwriting worksheets
- Phonics worksheets
- Phase 5 phonics
- KS2 SATs papers
- KS1 SATs papers
- Year 6 SATs
- Clauses
- Conjunctions
- Pronouns
- Determiners
- Modal verbs
- Apostrophes
- Punctuation worksheets
- Angles worksheets
- Symmetry worksheets
- Perimeter and area
- Rounding worksheets
- Roman numerals
- Negative numbers
- Money worksheets
- Sound buttons
- Tricky words
- Common exception words
- Browse all worksheets →
All rights reserved © Teach My Kids 2026. Site designed and built by BillyMedia